In my recent projects I have been experimenting a lot with pixel sorting. My concern was to find an algorithm that could handle 4 possible directions, have different directions in different areas, and run on the graphic card. In this article I will walk you through the technique I developed to handle such a problem. Source code is available at the end.
1) The constraints due to the usage of the GPU
First, it is important to understand the limitations of the GPU in the context of pixel sorting. Pixel sorting could be described as a glitchy effect which selectively orders the pixels of an image in a direction, where the pixels are ordered by luminance, grayscale, hue… Sorting is a well known subject in computer science, but existing algorithms are mostly designed for running on the CPU, because they require the manipulation of array of datas and the possibility to compare any value of the array to any other value of the same array, in any particulary order and so successively. On the other hand, GPU are designed to handle each value (a pixel of a texture) individually. On each iteration, a program is executed in parallel for all the pixels of an image, and the program outputs a value for each pixel. The new array is constructed by grouping all the previous values together, and the previous one gets lost in the process. To see why this is an issue in our case, take the following example:
We need to find an algorithm to sort in a ascending order an array of 8 numbers:
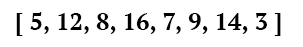
On each iteration, the algorithm will be run for each number of the array. It will have access to the whole array, its position in the array, and will have to output only 1 value. There can be any number of iterations, as long as at some point, the array stays the same after every iteration, and is in a sorted order. The inputs of our «fragment shader» :
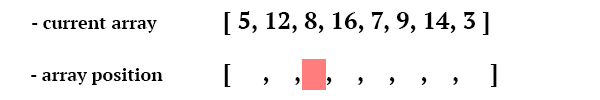
And the algorithm is expected to output 1 value, the new value of the array at its index:
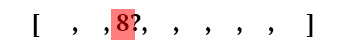
Visualization of an iteration on the GPU:
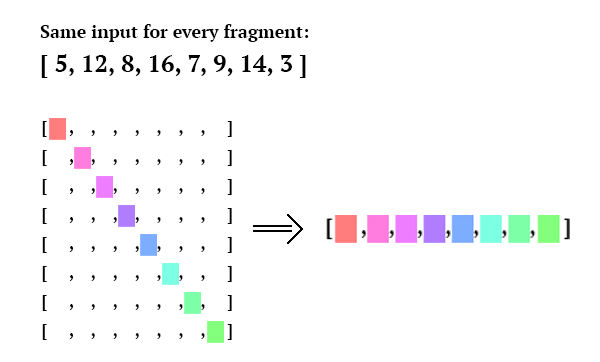
If we wanted our algorithm to be done after 1 iteration, we would need to compare each number to all the numbers in the array, sort them in ascending order, and output the number at the position of the fragment. In this particular case, there wouldn’t be any performance issue since we’re talking about 8 numbers sort; but imagine if we had 1000 (which will be the case when working on images). Also, on the GPU, it is only possible to get 1 value from the input array at a time, and it is an expensive operation: we want to avoid it as much as possible (this is called Sampling).
Also, because we lose the previous array after an iteration, we must ensure that the logic of our fragment shader stays non-destructive. If for instance, the fragment shader at position [0] should return 3, when it was previously 5, another fragment should return 5 so that it does not get lost after the iteration.
2) The Odd-even transposition sort
The Odd-even sort [1], also known as Brick sort, is an algorithm designed for use on parallel processors.
It functions by comparing all odd/even indexed pairs of adjacent elements in the list and, if a pair is in the wrong order (the first is larger than the second) the elements are switched. The next step repeats this for even/odd indexed pairs (of adjacent elements). Then it alternates between odd/even and even/odd steps until the list is sorted.
Wikipedia
This algorithm is pretty simple, and matches all the criteria we need. Let’s see how it would perform on our example:

This greatly simplifies our problem. Now, our sorting fragment shader can only sample 2 array positions: the one at its index and its right neighbor (or left depending on the parity of the iteration number). Then, given the direction of the sort, it can compare the 2 samples and swap their value if required.
For our algorithm to be working, we also need to implement a feedback mechanism, where the output of the sort is sent back as an input for the next iteration. This technique won’t be detailed in this article.
3) Writing a basic pixel sort shader
We now have all the tools to write a basic pixel sorting shader. Let’s find a mathematical way to define how to pick the pixels to compare: pick the neighbour of any pixel, given its coordinates. We will be working in pixel space coordinates to simplify the problem (1 pixel = 1 square unit). Let’s say we have a 16×16 image:
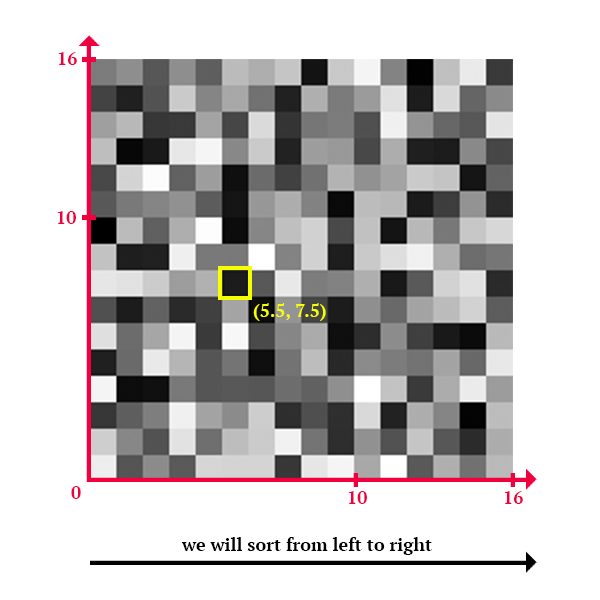
Horizontal neighbours of a pixel are either at its direct left or at its direct right. Mathemically speaking, if ![]() are the coordinates of the pixel of interest,
are the coordinates of the pixel of interest, ![]() the coordinates of the neighbour we want to find, then
the coordinates of the neighbour we want to find, then ![]() is either equal to
is either equal to ![]() or
or ![]() .
.
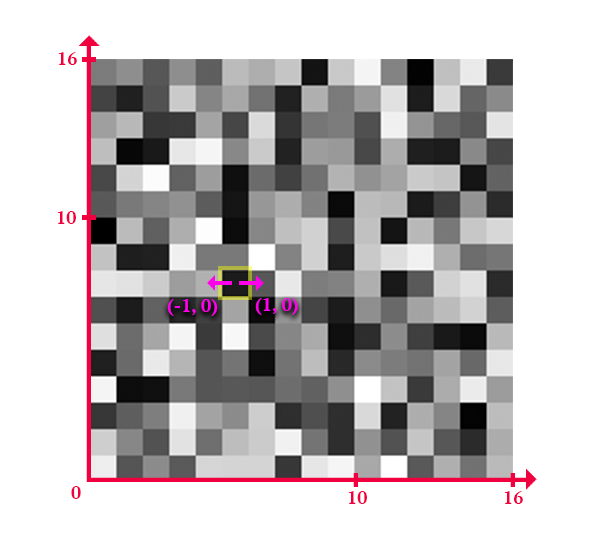
Therefore, the function to find ![]() from
from ![]() we’re looking for has the signature:
we’re looking for has the signature:
![Rendered by QuickLaTeX.com \[ f(P) = P' = P + \binom{1}{0} \cdot a\]](https://ciphrd.com/wp-content/ql-cache/quicklatex.com-22ed953b94a494df91a5d306a89f99a2_l3.png)
where
To find how to compute ![]() , we need to break down the odd-even sort algorithm. Pixels will be grouped by 2. Therefore,
, we need to break down the odd-even sort algorithm. Pixels will be grouped by 2. Therefore, ![]() will have opposite values every 1/2 pixel on the x-axis.
will have opposite values every 1/2 pixel on the x-axis.

Also, every 1/2 iteration of the algorithm, the directions needs to be inverted for the algorithm to make progress, as demonstrated in part 2. It is now possible to compute the value of ![]() . In the following formula, we’ll consider the coordinates of P to be integers. Let
. In the following formula, we’ll consider the coordinates of P to be integers. Let ![]() be the number of iterations of the algorithm:
be the number of iterations of the algorithm:
![]()
The 2 terms of this expression will both be either -1 or 1, and therefore flip
We now have a way to find the pixels we need to compare by sampling the input image at ![]() and
and ![]() . Also, given the sign of
. Also, given the sign of ![]() , we know in which direction the comparaison needs to be done. Quick reminder: when working with GLSL, coordinates will be between 0 and 1, so
, we know in which direction the comparaison needs to be done. Quick reminder: when working with GLSL, coordinates will be between 0 and 1, so ![]() needs to be divided by the resolution of the input texture.
needs to be divided by the resolution of the input texture.
The algorithmic solution is pretty straightforward. The implementation is available on Shadertoy, at the end of this section and at the end of the article.
The following video demonstrates the sort on a 8×1 pixels image, where pixels are sorted by grayscale. The example shows which pixels are compared by grouping them by color (red/blue).
Now that we know how to sort 1 line, we can sort any image, regardless of its size.
Great effects can be achieved using a threshold for the sort. If we prevent the swap from happening if one of the 2 pixels compared has a grayscale value inferior to a threshold, we can create «breaks» in the sorted result.
4) Using a vector field to map the transpositions
Currently, our algorithm is not versatile. The swap direction is hard-coded in the sorting shader, where we pick the pixels to be swapped along the x axis to the left or to the right given the parity of the frame number.
What we could do, instead, is generate a separate texture, which size is the same as the image we want to sort. In the sorting shader, we could use this texture to find which pixel should be compared to the active pixel, based on a direction encoded in the color components of the texture. The following illustration demonstrate this principle.
As a quick note, when displaying vector fields in the following examples, colors will look a bit weird. Because some vectors will have negative values (negative values can’t be displayed on a screen), black pixels can represent negative values. The x component is encoded in the RED channel, y component encoded in the GREEN channel.
To apply the vector field to the sorting algorithm, everything is pretty straightforward. Instead of computing ![]() , we can grab it from the vector field, at the same position as the pixel. Nothing else to change for now.
, we can grab it from the vector field, at the same position as the pixel. Nothing else to change for now.
Great, we can move to the next step. What if, instead of encoding [-1, 0] and [1; 0] in the vector field, we would encode [-1, 1] and [1; -1] ? Pixels should be swapped diagonally, thus the sort should be diagonal:
The filter is yellow because Red + Green = Yellow, [1, 1]. Black pixels are [-1, -1]. I also added a test to block the pixels on the borders on the y-axis, the same as on the x-axis.
What happens now if we want to sort the pixels vertically ? Rotating the filter and the vector field won’t be enough, because our sorting shader is currently using the sign of ![]() , which is now grabbed from the vector field, to find in which direction the swaps takes place. We will be working with 8 different directions (cardinal). We need a function to sort those 8 directions in 2 categories, and after the sort is applied we’ll just have to test the category to know in which direction the sort should be perfomed.
, which is now grabbed from the vector field, to find in which direction the swaps takes place. We will be working with 8 different directions (cardinal). We need a function to sort those 8 directions in 2 categories, and after the sort is applied we’ll just have to test the category to know in which direction the sort should be perfomed.
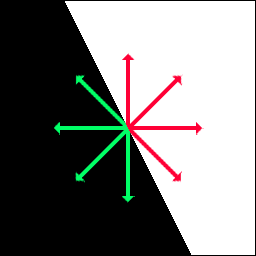
I came up with a custom function, that takes the ![]() and
and ![]() components of a vector from the vector field, and outputs -1 or 1:
components of a vector from the vector field, and outputs -1 or 1:
![]()
The following illustration demonstrates how this function sorts the different possible directions.
Now, instead of testing the sign of ![]() , we can test the sign of
, we can test the sign of ![]() . And suddenly, sorting pixels vertically works:
. And suddenly, sorting pixels vertically works:
An issue remains: what if we want the pixels to be sorted down ? After all, since we need half the vectors to be the opposite of the other half, there are no way for the sort shader to know in which direction we want to sort. However, we still have 2 components available in the texture that stores the vector field: Blue and Alpha. We will encode an information on the blue component: if the value > 0.5, we will swap the order of the sort by applying the swap the other way arround.
Last but not least: the sort is stopped on the borders, but we might need some cases where we want it to stop only on 1 axis, or maybe on different parts of the image. We could encode this informations in the alpha channel. If alpha > 0.5, we try to sort the texel, otherwise we don’t.
Okay, so before going further, it’s important we define a set of rules the vector field needs to follow in order for the sort algorithm to be non-destructive, and actually sort the pixels over time.
5) Well crafted vector fields for interesting effects
These are the rules I came up with for the vector fields:
- For every vector of the vector field, located at (x, y) pointing to (x’, y’), there must be a vector located at (x’, y’) pointing to (x, y). In other words, texels that should be swapped should have opposite vectors on the vector field.
- The vector field should at least have 2 states (A, B), where pairs of texels from state A should be different than the pairs from state B. This is required for the sort to be happening globally over time.
- Every component of the vectors from the vector field shouldn’t have a fractional part, so that we can be sure to land on another texel.
- As described previously, to offer diversity and control to the vector field, the blue component can encode the direction of the sort and the alpha component can encode whether the sort is possible or not.
If rule 1 isn’t followed, the sort could be destructive. Indeed, the algorithm requires that we compare pairs of texels. Let’s say we have 3 texels of interest, t1 t2 and t3. If we compare t1 with t2, but t2 gets compared to t3, we could lose one of the values due to the way the sort happens.
Given those, rules, let’s try to craft some interesting vector fields:
Notice how, in figure 16, because the rule 1 was broken (at the top, in the middle), we have this infinite generation of new texels. This is due to the fact that the sort happens in 1 way but not in the other, due to the fact that the vectors from the field are not opposite.
Crafting vector fiedls, a.k.a sorting filters, that keeps the continuity of the sort, can become quite a hard task. Every case should be taken into account, and even only 1 error at 1 position can result in the complete destruction of the whole original image.
There is A LOT of room for exploration. It is always good, when creating a new system, to find a way to generalize it so that it is possible to play with it in many different ways. I will be playing with it on my instagram, follow me if you’re interested in this type of content:
Follow me on instagram for more content6) Improvements
Preventing the sort from happening using the alpha channel is good, but the result is a bit weird: a part of the image gets ignored. Instead, we could prevent the sort from only happening in 1 direction.
Source code
The source code is available on ShaderToy:
HAVE FUN !
References
- Odd-even sort, Wikipedia
- Feedback, Computer Science Wiki

Hello